What we do

We study quantum many-particle systems for which topology, entanglement and interactions play important roles. These include fractional quantum Hall states, geometrically frustrated magnets, Weyl semimetals and various instances of flat band models. A common feature in these systems is that their low-energy quasiparticles bear little or no resemblance to their electronic constituents. Instead, the quasiparticles have intriguing properties such as fractional charge and statistics. To understand these notoriously complex systems we use a combination of analytical and numerical methods, beyond standard many-body theory, including exact diagnalization, field theory, strong coupling expansions etc., we occasionally adopt new methods and concepts from quantum information theory, including entanglement quantifiers and tensor networks, and contemporary mathematics, such as compressed sensing.

Why is this interesting and important?

Our research brings together several frontiers of basic science, while at the same time having the potential to provide the basis of future technological advances such as robust “topological quantum computers”.

To put our research in a broader perspective, note that while the majority of research is tending towards an ever higher degree of specialization, a desirable goal of science is to unify the description of the world around us at vastly different time, length and energy scales — and at levels of complexity ranging from elementary particles to biological systems. Contemporary physics provides a particularly beautiful example of such a unification between seemingly opposite frontiers, namely high energy particle physics on the one end, and condensed matter physics concerned with the emergent low energy collective behavior of ~10²⁴ constituents at the other end. Most saliently, it has been realized that many elusive particles hypothesized in the context of high-energy physics, such as Weyl and Majorana fermions, can emerge in the form of quasi-particles in the condensed matter setting. In fact, it turns out that condensed matter quasi-particles can be even more enigmatic as in the case of the fractional quantum Hall states where they are “anyons” possessing charge and statistics fundamentally different from what is expected given the constituent particles. Of special interest are non-Abelian anyons, whose hallmark is that a quantum state involving them is degenerate and can turn into an orthogonal state by adiabatically braiding quasi-particles. This has opened the prospect of storing quantum information in the global properties of these states, and has inspired ideas of using them as building blocks for quantum computers immune to any local disturbance, and thereby to decoherence which are the major obstacles to building large quantum computers. Still, no true table-top realizations of the needed states exist, and practically useful topological quantum computation remains a dream. Scrutinizing the fine-print it becomes clear that the extreme conditions — temperature of less than 1 Kelvin and magnetic fields of more than 10 Tesla, etc. — needed to realize fractional quantum Hall states in conventional semiconductor heterostructures will almost certainly exclude them from any practical use in computational devices.

However, the past years have witnessed a true paradigm shift in condensed matter physics whereby theory has taken the driver’s seat, feeding experimentalists with novel ideas for realizing topological states in a rich variety of systems. At the same time, the experimental technology has developed immensely in fields ranging from oxide interfaces to shaken optical lattices leading to an unparalleled experimental development. Particularly exciting are new ideas on how to engineer lattice analogues of fractional quantum Hall states, so-called fractional Chern insulators. These phases do not require an external magnetic field and may potentially persist — and harbor non-Abelian anyons — even at room temperature and pose exquisite challenges for theorists: the immensely complex quantum Hall problem of understanding the low energy behaviour of strong interactions within an flat band with non-trivial topology (Chern number) is further complicated by lattice effects, including of Berry curvature fluctuations and new competing instabilities, while it also facilitates exciting new features due to the possibility of having higher Chern numbers. Geometrical lattice frustration provides a conceptually different route to flat bands; there are many inequivalent ways of minimising the energy of antiferromagnetic spins of lattices made up from triangular units. The combination of lattice frustration, non-trivial band topology and interactions gives rise to a multitude of interesting low-energy phenomena which we are only beginning to understand at the same time as their interplay is very much relevant to materials such as the Pyrochlore iridates A₂Ir₂O₇.

In the pursuit for fractional Chern insulators it is highly encouraging to note that, during the past two years, the first integer (non-interacting) Chern insulators were experimentally realized without the need of magnetic fields in systems as diverse as magnetic topological insulators and optical lattices. In fact, non-interacting topological phases are also of continued theoretical interest not the least due to their interesting transport signatures, especially in precedes of including defects and disorder. Particularly interesting in this context are the Weyl semimetals — graphene’s topological cousin in three dimensions — which are gapless in the bulk yet support ample novel phenomena including surface Fermi arcs, a realisation of the chiral anomaly, negative magnetoresistance, nonlocal transport, and a quantum anomalous Hall effect.

Also on the conceptual side, the investigation of topological phases benefits from parallel developments in other fields of science. In particular, useful tools for the theoretical detection through the entanglement spectrum, and simulation in terms of tensor networks, build on insights from the field of quantum information.

In summary: it is a fascinating time to work on the physics of topological and strongly correlated quantum systems — the ongoing conceptual progress is revolutionising our fundamental understanding of matter as such at the same time as the experimental developments may provide the basis for future technological advances as exotic as topological quantum computers.

Below we sketch some of our own contributions to these topics and provide links to selected publications. For general reading on these topics we recommend the following review articles:

Non-Abelian anyons and topological quantum computation C. Nayak, S.H. Simon, A. Stern, M. Freedman and S. Das Sarma, Rev. Mod. Phys. 80, 1083 (2008).

Topological Flat Band Models and Fractional Chern Insulators E.J. Bergholtz and Z. Liu, Int. J. Mod. Phys. B 27, 1330017 (2013).

Recent developments in transport phenomena in Weyl semimetals P. Hosur and X.-L. Qi, C. R. Phys. 14, 857 (2013).

Colloquium: Topological insulators M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).

Topological insulators and superconductors X.-L. Qi and S.-C. Zhang, Rev. Mod. Phys. 83, 1057 (2011).

Our projects

Below we give brief descriptions of our main projects. A more complete list of publications can be found e.g. at NASA ADS.

Topological flat band models and fractional Chern insulators.

Lattice models combining dispersionless bands with non-trivial topology and strong interactions is one of our major research topics. Notable achievementsinclude construction of a microscopic model with flat bands with arbitrary Chern numbers, C, in pyrochlore slabs [1] and the subsequent discovery of C>1 fractional Chern insulators (FCIs) [2], which are particularly interesting as they lack faithful continuum analogues. We also provided a heuristic explanation for the precise occurrence of fractional quantum Hall (FQH) analogues in C=1 bands by relating to Haldane’s pseudopotential formalism [3], and clarified the precise relation between the lattice FCIs in C=1 bands and continuum FQH states Landau levelsby employing a recently developed Wannier basis for the lattice system [4]. Furthermore we identified a generic competing instability to compressible states in the lattice setting [3], and demonstrated that systems with long-range interactions are particularly promising in the context of non-Abelian FCIs. Currently we pursue several directions, some of which are outlined in our comprehensive review of the field [6].

[1] Flat bands with higher Chern number in pyrochlore slabs M. Trescher and E.J. Bergholtz, Physical Review B 86, 241111(R) (2012).

[2] Fractional Chern Insulators in Topological Flat Bands with Higher Chern Number Z. Liu, E.J. Bergholtz, H. Fan and A.M. Läuchli, Physical Review Letters 109, 186805 (2012).

[3] Hierarchy of fractional Chern insulators and competing compressible states A.M. Läuchli, Z. Liu, E.J. Bergholtz and R. Moessner, Physical Review Letters, 111, 126802 (2013).

[4] From fractional Chern insulators to Abelian and non-Abelian fractional quantum Hall states: adiabatic continuity and orbital entanglement spectrum Z. Liu and E.J. Bergholtz, Physical Review B 87, 035306 (2013).

[5] Non-Abelian Fractional Chern Insulators from Long-Range Interactions Z. Liu, E.J. Bergholtz and E. Kapit, Physical Review B 88, 205101 (2013).

[6] Topological Flat Band Models and Fractional Chern Insulators E.J. Bergholtz and Z. Liu, Int. J. Mod. Phys. B 27, 1330017 (2013).

Theory of the fractional quantum Hall effect.

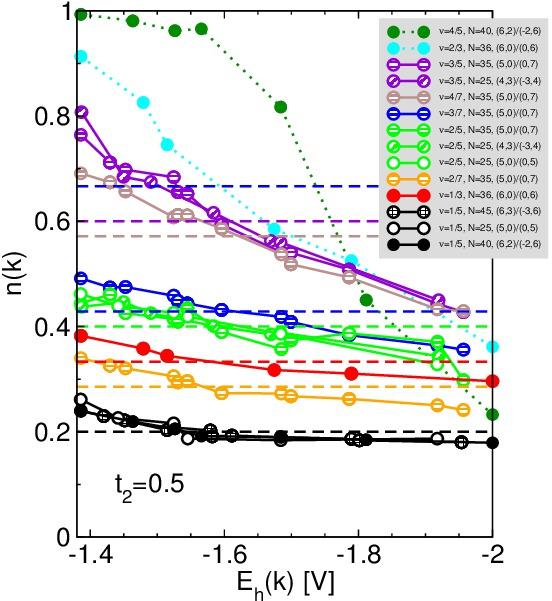
We also work on the theory of the fractional quantum Hall system in the continuum limit relevant for the semiconductor heterostructure experiments. Most saliently, we have developed the thin-torus perspective [7-10].In the thin-torus limit, the problem of strongly interacting particles within a Landau level is exactly solvable, and, remarkably, its gapped solutions are adiabatically connected to the bulk fractional quantum Hall states. The thin-torus approach is closely related to the the later ”patterns of zeros approach” developed by Wen and collaborators, and the Jack polynomial approach due to Bernevig and Haldane. 

In a related works, we also formulated new trial wave functions for the quantum Hall hierarchy using a conformal field theory construction [8,11]. In addition to extensive analytical work, we have developed a DMRG code for the FQH problem, as well an exact diagonalizationcode. In fact, it was via our initial DMRG simulations that we discovered the usefulness of studying the QH system on a thin torus [7,9]. Although most of this work was done long ago, during Emil’s PhD studies, we often make use of our background in this field — and every now and then we return to it, as when we found that certain truncated FQH Hamiltonians are exactly solvable in terms of matrix product states [12].

[7] Half-Filled Landau Level on a Thin Torus E.J. Bergholtz and A. Karlhede, Physical Review Letters 94, 026802 (2005).

[8] Microscopic theory of the quantum Hall hierarchy E.J. Bergholtz, M. Hermanns, T.H. Hansson and A. Karlhede, Physical Review Letters 99, 256803 (2007).

[9] Quantum Hall system in Tao-Thouless limit E.J. Bergholtz and A. Karlhede, Physical Review B 77, 155308 (2008).

[10] Pfaffian quantum Hall state made simple: multiple vacua and domain walls on a thin torus E.J. Bergholtz, J. Kailasvuori, E. Wikberg, T.H. Hansson and A. Karlhede, Physical Review B 74, 081308(R) (2006).

[11] Quantum Hall hierarchy wave functions--from conformal correlators to Tao-Thouless states E.J. Bergholtz, M. Hermanns, T.H. Hansson, A. Karlhede and S.F. Viefers, Physical Review B 77,165325 (2008).

[12] Exactly solvable fermion chain describing a ν=1/3 fractional quantum Hall state M. Nakamura, Z.-Y. Wang and E.J. Bergholtz, Physical Review Letters 109, 016401 (2012).

Geometrically frustrated magnets.

Geometrical frustration gives rise to a different type of flat bands. The recent theoretical prediction and subsequent experimental realization of classical analogues of magnetic monopoles in spin ice materials clearly show that such flat bands may also lead to topological phenomena. In our work, we focus on the interplay between geometrical lattice frustration, interactions and spin-orbit coupling on the quantum mechanical level where subtle quantum fluctuations lift the huge degeneracy leading to rich and complicated low energy behaviour. Notably, for the three-dimensional hyperkagome spin-1/2 Heisenberg magnet, motivated by the intriguing physics of Na₄Ir₃O_8, we put forward the possibility of a complex ordered valence bond crystal ground state with a huge unit cell [12]. This scenario predicts a number of thermodynamic signatures as well as low-energy excitations living on dimensionally reduced motifs. Ongoing work includes the study of pyrochlore magnets as well as layered systems with geometrical frustration.

 

[12] Symmetry Breaking on the Three-Dimensional Hyperkagome Lattice ofNa₄Ir₃O₈ E.J. Bergholtz, A.M. Läuchli and R. Moessner, Physical Review Letters 105, 237202 (2010).

Entanglement in topological states of matter.

The concept of entanglement is useful both for characterising topological states and in the context of efficient simulation methods.

In early works on the topic, wesignificantly improved the methods for numerically evaluating entanglement measures in FQH states by continuously varying the geometry, and thus the physical boundary between the system and the environment [13,14]. For the von Neumann entropy, our method improved the control of the entanglement scaling significantly, and the precision extraction of the topological part, γ, was improved by about an order of magnitude [14]. For the entanglement spectrum, this allowed us to obtain a microscopic understanding of the entanglement levels by connecting to the thin-torus limit and also to study the interplay between two spatially separated edges [13]. More recently, we have employed rigourous mathematical methods to demonstrated that the total amount of entanglement in topological states is truly non-universal and can be tuned to any value, yet the fact that there is an area law is topologically robust [15].

Tensor networks comprise a class of simulation methods whose power is based on the low entanglement in eigenstates of local Hamiltonians, i.e. the entanglement area law. We have employed the most successful of these methods, DMRG, which is developed for one-dimensional systems, to fractional quantum Hall states and fractional Chern insulators on finite cylinders [7,16]. Although the two-dimensional thermodynamic can never be reached in this setting it greatly increases the systems sizes that can be studied numerically compared to more conventional exact diagonalization schemes.

[13] Disentangling Entanglement Spectra of Fractional Quantum Hall States on Torus Geometries A.M. Läuchli, E.J. Bergholtz, J. Suorsa and M. Haque, Physical Review Letters 104, 156404 (2010).

[14] Entanglement Scaling of Fractional Quantum Hall states through Geometric Deformations A.M. Läuchli, E.J. Bergholtz and M. Haque, New Journal of Physics 12, 075004 (2010).

[15] Topological insulators with arbitrarily tunable entanglementJ.C. Budich, J. Eisert and E.J. Bergholtz, Physical Review B 89, 195120 (2014).

[16] Bulk-edge correspondence in fractional Chern insulators Z. Liu, D.L. Kovrizhin and E.J. Bergholtz, Physical Review B 88, 081106(R) (2013).

Weyl semimetals and quantum transport.

The progress in materials science has also spurred the interest in entirely different types of topological matter such as Weyl and Dirac semimetals. These can be seen as graphene’s topological cousins in three dimensions, they are gapless in the bulk yet support novel Fermi arcs on its surfaces. In recent work we have concentrated on quantum transport in the bulk and identified the Fano factor (the ratio of shot noise power and current) as an excellent indicator discriminating between a pseudoballistic regime with zero conductivity and a scale-independent conductance, and a diffusive regime for stronger disorder [17]. A generic feature of Weyl semimetals is that the low energy Weyl cones are tilted and anisotropic, which we have shown to have unusual signatures in shot noise experiments [18]. Presently we investigate the critical behaviour disordered Weyl semimetals, effects of interactions as well as the nature and signatures of defects and surface states (see also below).

[17] Quantum transport of disordered Weyl semimetals at the nodal point B. Sbierski, G. Pohl, E. J. Bergholtz and P. W. Brouwer, Physical Review Letters 113, 026602 (2014).

[18] Quantum transport in Dirac materials: signatures of tilted and anisotropic Dirac and Weyl cones M. Trescher, B. Sbierski, P.W. Brouwer and E.J. Bergholtz, arXiv:1501.04034.

Combining all of the above; topology enriched by frustration.

We recently discove

red that destructive interference due to local lattice frustration adds a novel twist to topology: adding Chern insulating layers in a suitably frustrated way generically leads to bands carrying higher Chern numbers [1,2] whose constant energy curves take the shape of Fermi arcs, localized to different surfaces depending on their quasi-moment

um [15]. Remarkably, if the slabs are thin enough, interactions within the Fermi arcs can indeed drive the system into fractional Chern insulators whose low-energy excitations are non-Abelian anyons! [2,15] This is is particularly relevant for pyrochlore slabs grown in the [111] directions. In fact, compared to more standard transition metal oxides compounds, notably perovskites, the actual growth or cleavage along the particularly interesting crystallographic [111] directions is considerably easier in the pyrochloresas this coincides with their natural cleavage planes which should greatly facilitate the fabrication of clean slabs. A further consequence of our work is that the Fermi arcs can in fact remain even when there are no Weyl nodes present in the bulk.

The study of the interplay between interactions, topology and geometrical frustration is still in its infancy, and we expect ample new physics to be uncovered in this context. Our theoretical investigations draw inspiration both from the synthesis of bulk materials, such as pyrochlore iridates A₂Ir₂O₇, as well as from the rapid development of growth techniques in fabricating high quality slabs/films/interfaces of oxide materials.

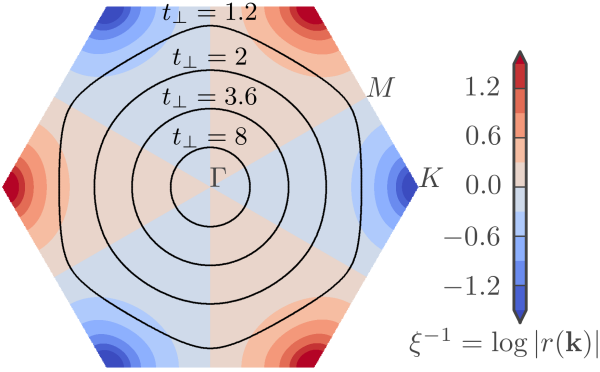
[15] Topology and Interactions in a Frustrated Slab: Tuning from Weyl Semimetals to C > 1 Fractional Chern Insulators E.J. Bergholtz, Z. Liu, M. Trescher, R. Moessner and M. Udagawa, Physical Review Letters 114, 016806 (2015).

_{Some other fun topics and future directions.}

Some of our work does not quite fit into the above topics, yet they concern the similar basic questions regarding the topology in many-particle quantum systems.

One example is our recent study of crystal and quasicrystal band structures which came as a reaction to claims that quasicrystals have protected edge states in direct analogy topological phases in higher dimensions. Our work explicitly showed that this claim is void; the numerically observed edge states in quasicrystals are due to fine tuning precisely as any (trivial) crystal can have zero energy states at the edges due to fine tuning rather than topology [16].

In a second recent project we employed compressed sensing in order to investigate how localized basis functions, a.k.a. Wannier functions, can possibly be in a given topological class [17]. This problem is largely unexplored, yet of great importance in context varying from first principles studies of topological materials to the “theoretical engineering” of topological phases.

With the benefit of theoretical research that we can rather quickly change directions, we always think of possible new topics. One such interesting direction concerns open and driven cold atom systems, and in particular the interplay between Hamiltonian and Liouvillian dynamics in the context of engineering novel steady states.

[16] Topological equivalence of crystal and quasicrystal band structures K.A. Madsen, E.J. Bergholtz and P.W. Brouwer, Physical Review B 88, 125118 (2013).

[17] Search for localized Wannier functions of topological band structures via compressed sensing J. C. Budich, J. Eisert, E. J. Bergholtz, S. Diehl and P. Zoller, Physical Review B 90, 115110 (2014).