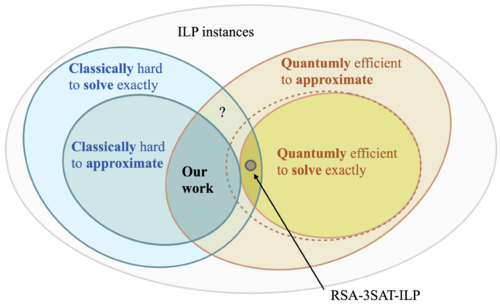
Combinatorial optimization - a field of research addressing problems that feature strongly in a wealth of practical and industrial contexts - has been identified as one of the core potential fields of applicability of near-term quantum computers. It is still unclear, however, to what extent variational quantum algorithms can actually outperform classical algorithms for this type of problems. In this work, by resorting to computational learning theory and cryptographic notions, we prove that fault-tolerant quantum computers feature a super-polynomial advantage over classical computers in approximating solutions to combinatorial optimization problems. Specifically, building on seminal work of Kearns and Valiant, we construct special instances of the integer programming problem (which in its most general form is NP-complete) that we prove to be hard-to-approximate classically but give an efficient quantum algorithm to approximate the optimal solution of those instances, hence showing a super-polynomial quantum advantage. This result shows that quantum devices have the power to approximate combinatorial optimization solutions beyond the reach of classical efficient algorithms.