The increasing availability of high-quality magnetic Weyl semimetals, for which the Weyl-node positions in the energy-momentum space depend on the magnetization direction, opens the possibility to have Weyl-semimetal superstructures where the node positions vary in space to form periodic patterns.

In a recent article

M. Breitkreiz and P. W. Brouwer, Phys. Rev. Lett. 130, 196602 (2023)

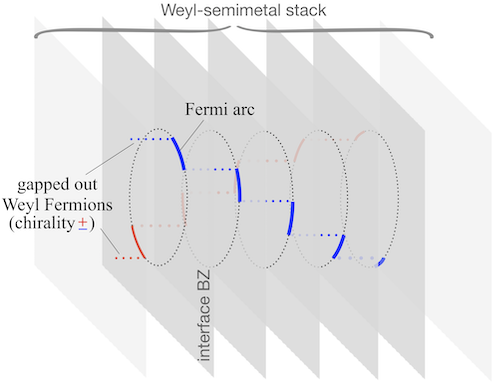
we predict a novel metallic state of matter that emerges in some of these superstructures. It is characterized by the presence of Weyl-Fermion chirality and the associated chiral anomaly, but with a full Fermi surface instead of isolated Weyl nodes. A concrete example on how such a metal can be constructed theoretically is illustrated in the Figure to the left: Consider a stack of Weyl semimetals with rotating Weyl-Fermion positions. The Weyl-semimetal topology applied to such a heterostructure dictates that the Weyl-Fermion positions (red/blue dotted lines) must be connected by Fermi-arc states that are localized to the interfaces (red/blue solid lines). The Weyl Fermions themselves suffer from finite-size gapping due to reflections at interfaces. As a result, the low-energy states are built entirely from Fermi arcs, which form the Fermi surface of this system (in the Brillouin zone reduced to the periodicity of the superstructure).

These "Fermi-arc metals" turn out to have unique, observable properties. The Landau level spectrum shows a gap between the lowest and the higher energy levels at arbitrarily low magnetic fields. This leads to a characteristic universal magnetoconductance and an "invisibility" of the Fermi surface in quantum-oscillation experiments --- a set of standard Fermi-surface-detecting techniques --- while it remains fully visible for other techniques, such as ARPES and non-oscillatory parts of response functions. Both effects break with the basic text-book description of metals. Furthermore, the form in which the Weyl-Fermion chirality occurs in Fermi-arc metals favors interaction-induced chiral symmetry breaking and thus opens a new route towards the realization of axions.