Quantum Oscillations
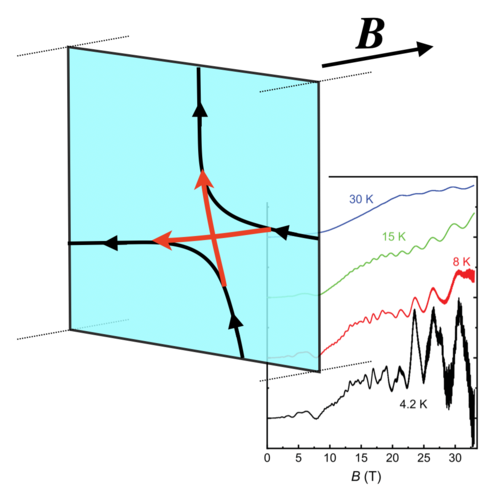
Oscillations of response functions in applied magnetic fields are one of the best studied manifestations of the quantum nature of electrons. Quantum-oscillation measurements (Shubnikov-de Haas and de Haas-van Alphen effects) belong to the text-book-standard experimental tools in condensed matter. Exciting new twists arise in topological matter, mainly due to three facts, (i) phase shifts of the oscillations caused by topological singularities in the band structure, (ii) topological surface states, and (iii) magnetic breakdown — magnetic-field induced quantum tunneling between adjacent bands. Our research addresses all three branches. Specifically, we explored phase shifts at a variety of band singularities (i) and identified a family of singularities that give rise to universally quantized phase shifts [1] determined by the topological invariant. Magnetic breakdown (ii) has been revealed experimentally in a family of nodal-line semimetals in the Radboud Magnet Lab, flanked by theoretical support from our side [2, 3, 4]. Most recently, we explored how topological surface states (iii) enable novel magnetic breakdown effects [5] and lead to unique quantum-oscillation signatures in transport that are not the usual Shubnikov-de Haas effect [6].
[1] “Phase shift of cyclotron orbits at type-I and type-II multi-Weyl nodes”, M. Breitkreiz, N. Bovenzi, and J. Tworzydło, Phys. Rev. B 98, 121403(R) (2018). Rapid communication
[2] “Electron-hole tunneling revealed by quantum oscillations in the nodal-line semimetal HfSiS”, M. R. van Delft, S. Pezzini, T. Khouri, C. S. A. Müller, M. Breitkreiz, L. M. Schoop, A. Carrington, N. E. Hussey, and S. M. Wiedmann, Phys. Rev. Lett. 121, 256602 (2018).
[3] “Determination of the Fermi surface and field-induced quasi-particle tunneling around the Dirac nodal-loop in ZrSiS”, C. S. A. Müller, T. Khouri, M. R. van Delft, S. Pezzini, Y.-T. Hsu, J. Ayres, M. Breitkreiz, L. M. Schoop, A. Carrington, N. E. Hussey, and S. M. Wiedmann, Phys. Rev. Res. 2, 023217 (2020).