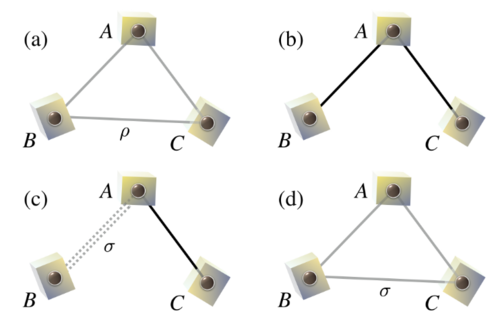
The theory of the asymptotic manipulation of pure bipartite quantum systems can be considered completely understood: The rates at which bipartite entangled states can be asymptotically transformed into each other are fully determined by a single number each, the respective entanglement entropy. In the multi-partite setting, similar questions of the optimally achievable rates of transforming one pure state into another are notoriously open. This seems particularly unfortunate in the light of the revived interest in such questions due to the perspective of experimentally realizing multi-partite quantum networks.In fact,  the question of what rates are achievable in multi-partite entanglement transformations emerged in the early 2000 years as one of the key questions in quantum information theory. It has not found a comprehensive answer to date.

In this work, we report substantial progress on this long-standing question by deriving surprisingly simple upper and lower bounds on the rates that can be achieved in asymptotic multi-partite entanglement transformations. These bounds are based on ideas of entanglement combing and state merging. We identify cases where the bounds coincide and hence provide the exact rates. As an example, we bound rates at which resource states for the cryptographic scheme of quantum secret sharing can be distilled from arbitrary pure tripartite quantum states, providing further scope for quantum internet applications beyond point-to-point.This work has been published in the Physical Review Letters.