New work on the complexity of the sign problem in Quantum Monte Carlo (QMC) has been published in the Science Advances.

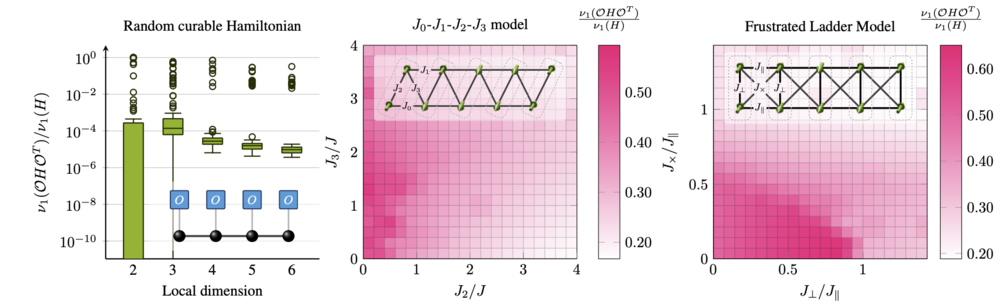
QMC methods are the gold standard for studying equilibrium properties of quantum many-body systems - their phase transitions, ground and thermal state properties. However, in many interesting situations QMC methods are faced with a sign problem, causing the severe limitation of an exponential increase in the sampling complexity and hence the run-time of the QMC algorithm. In this work, we develop a systematic, generally applicable, and practically feasible methodology for easing the sign problem by efficiently computable basis changes and use it to rigorously assess the sign problem. Our framework introduces measures of non-stoquasticity that - as we demonstrate analytically and numerically - at the same time provide a practically relevant and efficiently computable figure of merit for the severity of the sign problem. We show that those measures can practically be brought to a good use to ease the sign problem. To do so, we use geometric algorithms for optimization over the orthogonal group and ease the sign problem of frustrated Heisenberg ladders. Complementing this pragmatic mindset, we prove that easing the sign problem in terms of those measures is in general an NP-complete task for nearest-neighbour Hamiltonians and simple basis choices by a polynomial reduction to the MAXCUT-problem. Intriguingly, easing remains hard even in cases in which we can efficiently assert that no exact solution exists.

A press release can be found here.