Work on holographic area laws in PRL
The area law conjecture states that the entanglement entropy of a region of space in the ground state of a gapped, local Hamiltonian only grows like the surface area of the region. In new work going to press in the Physical Review Letters show that, for any quantum state that fulfills an area law, the reduced quantum state of a region of space can be unitarily compressed into a thickened surface of the region. If the interior of the region is lost after this compression, the full quantum state can be recovered to high precision by a quantum channel only acting on the thickened surface. The thickness of the boundary scales inversely proportional to the error for arbitrary spin systems and logarithmically with the error for quasi-free bosonic systems. Our results can be interpreted as a single-shot operational interpretation of the area law. The result for spin systems follows from a simple inequality showing that probability distributions with low entropy can be approximated by distributions with small support, which we believe to be of independent interest. We also discuss an emergent approximate correspondence between bulk and boundary operators and the relation of our results to tensor network states.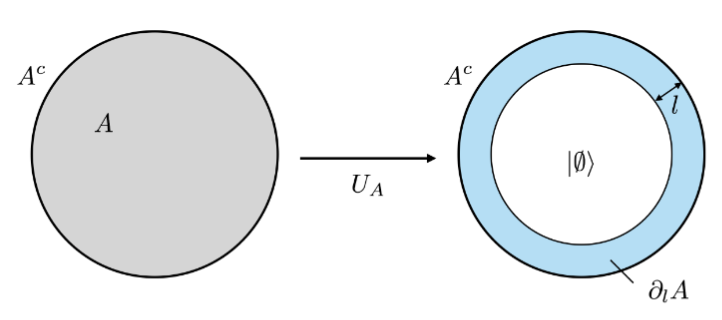
News from May 16, 2019