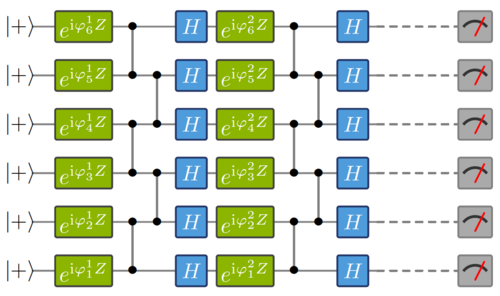
Demonstrating a quantum computational speedup is a crucial milestone for near-term quantum technology. Recently, quantum simulation architectures have been proposed that have the potential to show such a quantum advantage, based on commonly made assumptions. The key challenge in the theoretical analysis of this scheme - as of other comparable schemes such as boson sampling - is to lessen the assumptions and close the theoretical loopholes, replacing them by rigorous arguments. In this work, we prove two open conjectures for these architectures for Hamiltonian quantum simulators: Anticoncentration of the generated probability distributions and average-case hardness of exactly evaluating those probabilities. The latter is proven building upon recently developed techniques for random circuit sampling. For the former, we develop new techniques that exploit the insight that approximate 2-designs for the unitary group admit anticoncentration. We prove that the 2D translation-invariant, constant depth architectures of quantum simulation form approximate 2-designs in a specific sense, thus obtaining a significantly stronger result. Our work, freshly published in the Physical Review Letters, provides the strongest evidence to date that Hamiltonian quantum simulation architectures are classically intractable.