Initially, quantum anomalies have been theoretically predicted in the context of elementary-particle quantum-field theory. In particular, the chiral anomaly (also called Adler-Bell-Jackiw anomaly) arises when the mass of a spin-1/2 Dirac fermion is exactly zero, in which case the Dirac fermion “falls apart” into two Weyl fermions of opposite chirality. Since the Weyl fermions appear completely decoupled in the action, classically one would expect conservation of particle numbers of eachWeyl fermion species separately. On the quantum-mechanical level, however, the two species

turn out to be coupled by the electromagnetic field, the application of which allows to change the relative particle number. So far the chiral anomaly has not been experimentally observed in the context of elementary particles, all observed fermions are massive and thus don’t fall apart into Weyl fermions. In condensed matter, however, some crystals allow to realize Weyl fermions and also their various generalizations (such as with higher spin) as topologically protected quasiparticles (-> review paper). These socalled topological (semi)metals have been experimentally discovered in 2015 (-> discovery paper), which triggered an enormous research activity to understand quantum-anomaly manifestations in condensed matter and to explore all its consequences on a fundamental level, as well as with regard to novel technological applications.

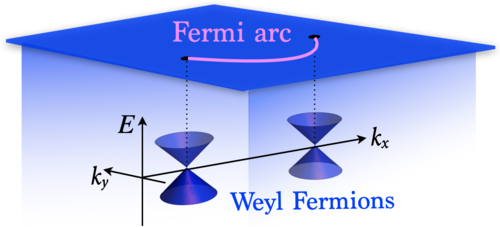
Importantly, on the material surface of the anomaly-hosting material, the quantum anomaly manifests in form of topological surface states that form Fermi arcs, which connect projections of Weyl fermions of opposite chiralities in the surface Brillouin zone, as illustrated in the Figure.

In this group we explore anomalous transport phenomena that are associated with Fermi arcs and/or the interplay of Fermi arcs with bulk Weyl fermions [1,2,3]. We revealed, in particular, that Fermi arcs can make a large contribution to dc transport [1, 3]. This phenomenon is in agreement with experiments and makes topological-metal thin films being considered as potentially better conductors than copper for semiconductor interconnects.

Moreover, the spatial confinement of Fermi arcs allows to shape the response in nano- and heterostructures based on topological matter [2, 4]. In [4] we predict the novel metallic state, Fermi arc metal (-> read more), in superstructures based on topological metals, where the well-conducting Fermi arcs populate the whole material bulk rather than just the surface. On the other hand, in Ref. [5] we exemplify how the combination of spatial confinement with proximitized superconductivity can be used to shape dissipationless transport.

[1] “Large contribution of Fermi arcs to the conductivity of topological metals”, M. Breitkreiz and P. W. Brouwer, Phys. Rev. Lett. 123, 066804 (2019).

[2] “Parabolic Hall effect due to co-propagating surface modes”, M. Breitkreiz, Phys. Rev. Res. 2, 012071(R) (2020). 

[3] “Chiral Anomaly Trapped in Weyl Metals: Nonequilibrium Valley Polarization at Zero Magnetic  Field”, P. M. Perez-Piskunow, N. Bovenzi, A. R. Akhmerov, and M. Breitkreiz, SciPost Physics 11, 046 (2021).

[4] "Fermi-Arc Metalls", M. Breitkreiz and P.W. Brouwer, Phys. Rev. Lett. 130, 196602 (2023).

[5] “Equilibrium current in a Weyl-semimetal - superconductor heterostructure”, K. A. Madsen, P. W. Brouwer, and M. Breitkreiz, Phys. Rev. B 104, 035109 (2021).