Three group publications have been published in a row in PRX Quantum, in topics of quantum error correction and fault tolerance, quantum learning and quantum complexity.

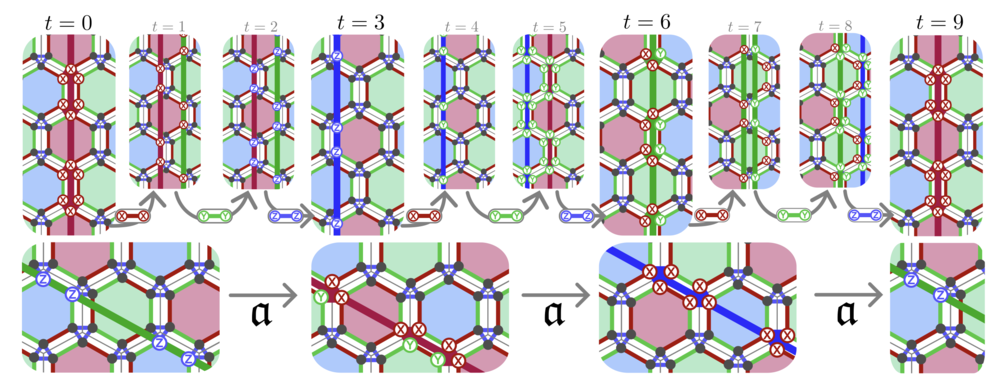
XYZ ruby code: Making a case for a three-colored graphical calculus for quantum error correction in spacetime 
PRX Quantum 6, 010360 (2025)

Analyzing and developing new quantum error-correcting schemes is one of the most prominent tasks in quantum computing research. In such efforts, introducing time dynamics explicitly in both analysis and design of error-correcting protocols constitutes an important cornerstone. In this work, we present a graphical formalism based on tensor networks to capture the logical action and error-correcting capabilities of any Clifford circuit with Pauli measurements. We showcase the formalism on new Floquet codes derived from topological subsystem codes, which we call XYZ ruby codes. Based on the projective symmetries of the building blocks of the tensor network we develop a framework of Pauli flows. Pauli flows allow for a graphical understanding of all quantities entering an error correction analysis of a circuit, including different types of QEC experiments, such as memory and stability experiments. We lay out how to derive a well-defined decoding problem from the tensor network representation of a protocol and its Pauli flows alone, independent of any stabilizer code or fixed circuit. Importantly, this framework applies to all Clifford protocols and encompasses both measurement- and circuit-based approaches to fault tolerance. We apply our method to our new family of dynamical codes which are in the same topological phase as the 2+1d color code, making them a promising candidate for low-overhead logical gates. In contrast to its static counterpart, the dynamical protocol applies a Z3 automorphism to the logical Pauli group every three timesteps. We highlight some of its topological properties and comment on the anyon physics behind a planar layout. Lastly, we benchmark the performance of the XYZ ruby code on a torus by performing both memory and stability experiments and find competitive circuit-level noise thresholds of 0.18%, comparable with other Floquet codes and 2+1d color codes.

Complexity-constrained quantum thermodynamics
PRX Quantum 6, 010346 (2025)

Quantum complexity measures the difficulty of realizing a quantum process, such as preparing a state or implementing a unitary. We present an approach to quantifying the thermodynamic resources required to implement a process if the process’s complexity is restricted. We focus on the prototypical task of information erasure, or Landauer erasure, wherein an 𝑛-qubit memory is reset to the all-zero state. We show that the minimum thermodynamic work required to reset an arbitrary state in our model, via a complexity-constrained process, is quantified by the state’s complexity entropy. The complexity entropy therefore quantifies a trade-off between the work cost and complexity cost of resetting a state. If the qubits have a nontrivial (but product) Hamiltonian, the optimal work cost is determined by the complexity relative entropy. The complexity entropy quantifies the amount of randomness a system appears to have to a computationally limited observer. Similarly, the complexity relative entropy quantifies such an observer’s ability to distinguish two states. We prove elementary properties of the complexity (relative) entropy. In a random circuit—a simple model for quantum chaotic dynamics—the complexity entropy transitions from zero to its maximal value around the time corresponding to the observer’s computational-power limit. Also, we identify information-theoretic applications of the complexity entropy. The complexity entropy quantifies the resources required for data compression if the compression algorithm must use a restricted number of gates. We further introduce a complexity conditional entropy, which arises naturally in a complexity-constrained variant of information-theoretic decoupling. Assuming that this entropy obeys a conjectured chain rule, we show that the entropy bounds the number of qubits that one can decouple from a reference system, as judged by a computationally bounded referee. Overall, our framework extends the resource-theoretic approach to thermodynamics to integrate a notion of time, as quantified by complexity.

This work has been covered in PRX Quantum and in Quantum Frontiers.

Tomography of parametrized quantum states
PRX Quantum 6, 020346 (2025)

Characterizing quantum systems is a fundamental task that enables the development of quantum technologies. Various approaches, ranging from full tomography to instances of classical shadows, have been proposed to this end. However, quantum states that are being prepared in practice often involve families of quantum states characterized by continuous parameters, such as the time evolution of a quantum state. In this work, we extend the foundations of quantum state tomography to parametrized quantum states. We introduce a framework that unifies different notions of tomography and use it to establish a natural figure of merit for tomography of parametrized quantum states. Building on this, we provide an explicit algorithm that combines signal processing techniques with a tomography scheme to recover an approximation to the parametrized quantum state equipped with explicit guarantees. Our algorithm uses techniques from compressed sensing to exploit structure in the parameter dependence and operates with a plug and play nature, using the underlying tomography scheme as a black box. In an analogous fashion, we derive a figure of merit that applies to parametrized quantum channels. Substituting the state tomography scheme with a scheme for process tomography in our algorithm, we then obtain a protocol for tomography of parametrized quantum channels. We showcase our algorithm with two examples of shadow tomography of states time-evolved under an NMR Hamiltonian and a free fermionic Hamiltonian.