SHG by a surface of charged water microdroplet

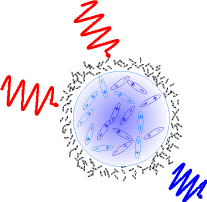
Fig. 1 Two red photons incident on a
water droplet suspended in air.
Strong SHG cannot be expected.

In dipole approximation Second Harmonic Generation (SHG) is forbidden in centrosymmetric media like liquids or gases. For this reason, Second Harmonic (SH) emission of water microdroplet is strictly surface related, where centrosymmetry of material is inherently violated. This situation is schematically depicted in Fig. 1.

Surface SHG is related to macroscopic non-linear polarization P_surf^2ω. It is proportional to the second order susceptibility and a square of incident electric field E. Omitting tensor notation one can write:

.

E_surf^2ω is typically too weak to induce a measurable signal. This situation is different in vicinity of surface charge as depicted in Fig. 2.

 

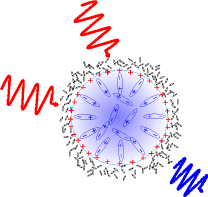
Fig. 2 Two red photons incident on a
charged water droplet. Strong SHG
can be expected due to orientation of
water dipoles.

Electric charges induce electrostatic field E₀, which penetrates droplet interior orienting water dipoles. This gives rise to nonzero third order susceptibility, . The magnitude of is calculated as thermodynamic average over all possible orientations of dipole moments and is related to their second and third order polarizability. Bulk water contribution to the second order polarization is described by formula:

.

P_bulk^2ω must be calculated as integral from the droplet center to its surface (from r=0 to r=R). Physically this mathematical operation is equivalent to difference of electric potential between these two points:

.

Setting reference potential inside the droplet to zero (Φ(0)=0) one can see that bulk polarization is directly proportional to surface potential Φ(R):

.

According to Gouy-Chapman model the surface potential is equal to:

,

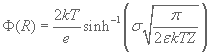where k is the Boltzmann constant, T is a temperature in Kelvin, Z is the electrolyte specific valency, σ is the surface charge density and ε is the relative dielectric emissivity of the medium.

Gouy-Chapman model was originally developed for planar interfaces and in principle should not be applicable for spherically shaped microdroplets. We must not forget, however, that for large micrometer sized droplets, the curvature of their surface is negligible on molecular scale of water dipoles and approximation of planar interface is well fulfilled.

Taking into account both surface and charge related contributions total SH field of electrified water microdroplet is proportional to the sum of two factors:

.

Therefore, the SH signal from microdroplet can be used to obtain information about its surface potential and charge.