Propagation
Propagation of a TW laser pulse in the atmosphere
Response of air to incoming electromagnetic radiation can be described in terms of induced macroscopic polarization P. In many cases this response is linear (proportional to applied electric field E), however, illumination by a short fs pulse having several tens of mJ energy is capable to induce non-linear response. Mathematically non-linear response of P requirers expansion of effective susceptibility ![]() in a power series. Since in centrosymmetric media like air the condition of P(-E)=-P(E) must be satisfied all even order expansion terms must be a priori set to zero. The first non-linear term includes a third order susceptibility
in a power series. Since in centrosymmetric media like air the condition of P(-E)=-P(E) must be satisfied all even order expansion terms must be a priori set to zero. The first non-linear term includes a third order susceptibility![]() :
:
![]() .
.
Changes of material's susceptibility impose changes of its dielectric permitivity ε. Since ε=ε0(1+Χ), the effective dielectric permitivity εeff is express by a quadratic equation, namely:
![]() .
.
Dividing it by ε0 and calculating a square root retrieves a modified refractive index of air:
![]() ,
,
where n0 is the linear refractive index of air and n2 is the non-linear refractive index of air. Note that non-linear modification of the effective refractive index depends on incoming light intensity I. Above equation is valid not only for air but many other centrosymmetric materials. It reflects a tendency of the medium to become optically thicker under illumination by intense light pulses. Such effect is known as the Kerr effect.
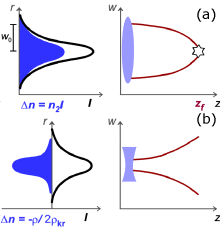
Fig. 1 Schematic representation of
(a) self-focusing and (b) defocusing
The Kerr effect can overcome natural diffraction of the beam initiating its self-focusing (SF). This phenomenon is widely observed with Gaussian or semi-Gaussian beams, for which the intensity distribution forms, so called, converging Kerr-lens (Fig. 1). To estimate the critical power Pcrit of SF the equilibrium between diffraction and Kerr self-focusing is assumed. For air and commonly used laser wavelength of 800 nm Pcrit ~ 3 GW.
The intensity inside self-focusing beam increases with a propagation distance and eventually leads to efficient plasma generation due to Multi-Photon Ionization (MPI) of nitrogen and oxygen molecules. MPI is believed to be a dominant ionization process, because collisions can be neglected in an ultra short femtosecond time scale and intensity required for tunnel ionization is much higher.
The role of unbounded electrons in plasma is often expressed in terms of the plasma frequency ωp. This quantity sets the boundary in a frequency domain distinguishing between photons, which are highly (photon frequency above plasma frequency) and rarely (photon frequency below plasma frequency) absorbed by plasma. The electron density corresponding to the plasma frequency is called critical density ρcrit:
![]() .
.
In the equation above me corresponds to the electron rest mass, e is the electron charge and ε is the dielectric permitivity. Using the critical density it is possible to show that the plasma contribution to the dielectric permitivity is negative. This means that the presence of free electrons lowers the air refractive index, namely:
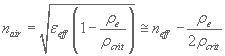 .
.
Because the MPI rate is a power function of the laser intensity (the power index corresponds to the multi-photon absorption order) the most dense plasma will be created in the central part of the self-focusing beam. In this way the electron density gradient is built, which as schematically depicted in Fig. 1, tends to defocus the beam forming akin of diverging lens counteracting Kerr-lens focusing. Taking into account both Kerr and plasma contribution the effective refractive index of air can be expressed in a form:
![]()

Fig. 2 A digital camera image of
multiple filamentation within a
fs-laser beam
Propagation of the fs-laser pulse in the air with modified refractive index is much different compared to the linear propagation. At first, the beam diameter undergoes a gradual transverse suppression initiated by Kerr-lens. Near the focus the E-field rapidly increases and efficient MPI takes place. Arising plasma retards Kerr-focusing and guides the energy in a stable filament, which is clearly distinguishable from the rest of the beam. From this moment small-scale, consecutive convergence and divergence stabilizes the filament sustaining it on distances much longer then its Rayleigh range. If the pulse power significantly exceeds Pcrit not only one, but many filaments are formed (Fig. 2). They are typically randomly arranged and their position is mainly determined by fluctuations of a beam transverse profile. The fluctuations act as micro Kerr-lenses concentrating the energy, which is successively clamped by each of filaments.
It is worth noting that the air filaments are always similar to one another. Their diameter is variable between 70-100 μm. Light intensity inside a filament varies between 1013-1014 W/cm2 and is mainly set by the MPI. Finally, the plasma density inside the filament is approximately 1016-1017 cm-3, which is only two orders of magnitude less than the air density.

Fig. 3 Conical emission resulting
from multiple filaments
Filament are always accompanied by many non-linear optical phenomena including odd harmonics generation, four wave mixing, self-phase modulation and spectrally broad, coherent white-light supercontinuum. Supercontinuum is partially emitted in a form of concentric cones called conical emission (Fig. 3). These non-linear phenomena are very interesting for various applications. For example, supercontinuum has been used for broadband atmospheric absorption spectroscopy, which as compared to Sun photometry is performed actively.