Physics

The quantum physicists at Freie Universität Berlin are currently participating in 10 large research consortia funded by the European Research Coulcil and the Federal Ministry of Education and Research: DebuQC, RealistiQ, HYBRID, QPIC-1, PhoQuant, MUNIQC, QSolid, QR.X, DAQC and FermiQP.

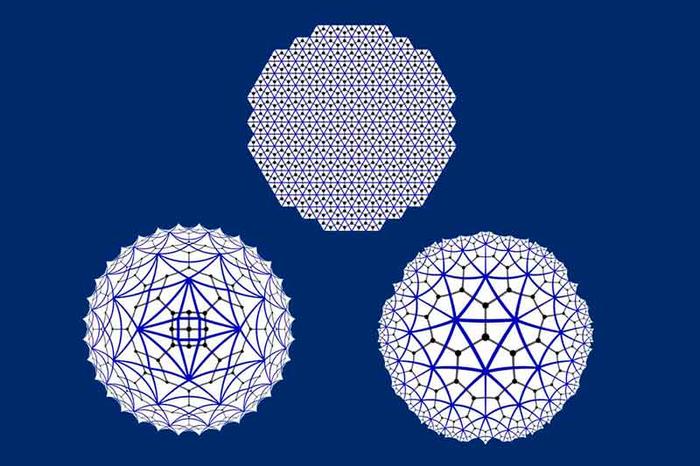
Complex Quantum Systems

The physical world that we encounter in our everyday experience exhibits a remarkable degree of complexity and richness of phenomena. It has long been noted that this apparent complexity is not necessarily a consequence of the underlying physical laws being complicated. In sharp contrast, this enormous complexity may arise from very basic local interactions. This is already true in the classical world: Fascinatingly complex features and patterns can emerge in nature from the simplest conceivable rules. This is even more so the case for physical systems with many degrees of freedom in which quantum phenomena become relevant. Quantum systems include the entire microscopic world, such as elementary particles and atoms, but also nanoscale electric conductors, semiconductors, large molecules, or certain materials whose macro-scale properties are determined by micro-scale quantum mechanical interactions. That is to say, this is expected to be true for complex quantum systems.

Our department is involved in a wide range of research activities on complex quantum systems, devoted to research in modern condensed matter physics and quantum information. This field of research includes the study of phenomena such as nanomagnetism, mesoscopic superconductivity and quantum chaos. In the focus of attention are physical systems ranging from naturally occurring ones, such as electronic systems with strong correlations or complex materials, to precisely engineered ones, such as Majorana devices, trapped ions and cold atomic gases, relevant in notions of quantum information. A joint feature is that complex quantum systems have intriguing properties which are in general difficult to predict, despite the simplicity of interactions. This complexity can be made a virtue, however, as such systems have practical applications. One such application is constituted by quantum simulators, devices that have the potential for outperforming even the fastest supercomputers available to date.

Common to a theoretical approach to the study of complex quantum systems is the mindset of putting concepts and ideas into the center of attention. Notions of transport are such concepts. So are notions of entanglement, so correlations that are in a precise sense stronger than classically attainable. In fact, we observe currently an exciting development that ideas of condensed matter physics - the study of materials and natural physical systems - and that of quantum information - the study of highly engineered quantum systems, exploiting quantum effects - are beginning to merge. The research activities in Berlin are particularly strong at this fresh interaction between the fields.

Our Research Methods

• Density Functional Theory (DFT)

• Transport and scattering theory

• Modelling of non-equilibrium states and their properties

• Methods of quantum information

• Tensor Networks