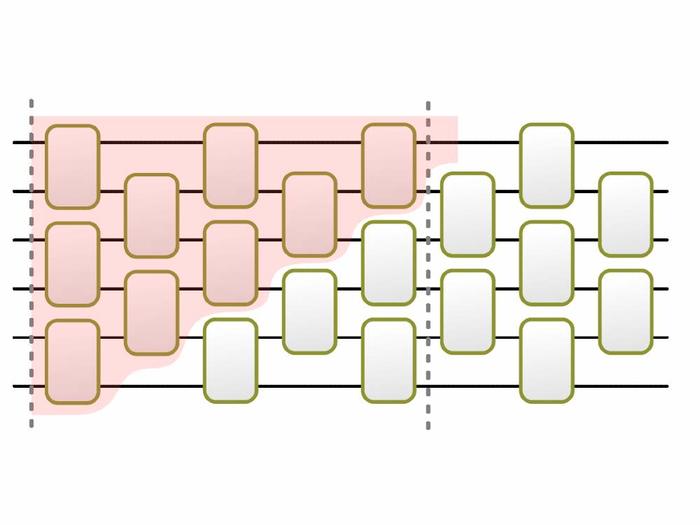
Quantenkomplexität wächst linear für exponentiell lange Zeiten
The Brown Susskind conjecture for random circuits postulates a linear growth of the circuit complexity, until a time exponential in the system size.
Bildquelle: DOI 10.1038/s41567-022-01539-6
Neue Publikation in “Nature Physics”: Die Quantenphysiker und Quantenphysikerinnen von der Freien Universität und der Harvard University belegen die Brown und Susskinds Vermutung zum Wachstum von Komplexität und finden damit einen Weg, eine bisher noch nicht überprüfte Annahme nachzuweisen. Für den Erstautor Jonas Haferkamp ist die Publikation ein krönender Abschluss seiner Promotion in der Arbeitsgruppe von Prof. Dr. Jens Eisert.
News vom 28.03.2022
„Wir haben eine überraschend einfache Lösung für ein wichtiges Problem in der Physik gefunden“, sagt Prof. Jens Eisert, theoretischer Physiker an der Freien Universität Berlin und am Helmholtz-Zentrum Berlin. Rein analytisch, nur mit Stift und Papier, ist es den Berliner Physikern Jonas Haferkamp, Philippe Faist, Naga Kothakonda und Jens Eisert zusammen mit Nicole Yunger Halpern (Harvard, inzw. Maryland) gelungen, eine Vermutung zu beweisen, die große Auswirkungen auf komplexe Quanten-Vielkörpersysteme besitzt. „Das spielt zum Beispiel eine Rolle, wenn man das Volumen von Schwarzen Löchern oder auch Wurmlöchern beschreiben will“, erklärt Jonas Haferkamp, der bei Eisert promoviert und Erstautor der Arbeit ist.
Komplexe Quanten-Vielkörpersysteme lassen sich durch Schaltungen aus Quanten-Bits nachbauen. Die Frage ist jedoch: Wie viele elementare Operationen sind nötig, um den gewünschten Zustand zu erreichen? Die minimale Anzahl an Operationen - die Komplexität des Systems – scheint stets am Wachsen zu sein. Die Physiker Adam Brown und Leonard Susskind von der Stanford Universität formulierten diese Intuition als eine mathematische Vermutung: Die Quantenkomplexität eines Vielteilchensystems sollte zunächst linear wachsen für astronomisch lange Zeiten und dann in einem Zustand maximaler Komplexität für eine noch längere Zeit verharren.
Das Forschungsteam hat nun gezeigt, dass die Quantenkomplexität von Zufallsschaltungen tatsächlich mit der Zeit linear ansteigt, bis sie zu einem Zeitpunkt gesättigt ist, der exponentiell zur Systemgröße ist. Solche Zufallsschaltungen sind ein mächtiges Modell für die Dynamik von Vielteilchensystemen. Die Schwierigkeit der Vermutung kommt daher, dass man kaum ausschließen kann, dass es „Abkürzungen“ gibt, also Schaltkreise mit viel geringerer Komplexität als erwartet. „Unser Beweis ist eine überraschende Kombination aus geometrischen Methoden und solchen aus der Quanteninformationstheorie. Dieser neue Zugang macht es möglich, die Vermutung für die überwältigende Mehrheit von Systemen zu lösen, ohne das notorisch schwierige Problem für individuelle Zustände angehen zu müssen“, sagt Haferkamp.
„Unsere Ergebnisse bieten eine solide Grundlage für das Verständnis der physikalischen Eigenschaften chaotischer Quantensysteme, von schwarzen Löchern bis hin zu komplexen Vielteilchensystemen“, kommentiert Eisert.
Schlagwörter
- Brown Susskind
- chaotische Quantensysteme
- Jens Eisert
- Jonas Haferkamp
- Nature Physics
- Publikation
- Quanten-Bits
- Quantenkomplexität
- Quantenphysik
- Vielteilchensysteme
- Zufallsschaltungen